Faktör Analizinin tanıtımını ve SPSS’te nasıl yapıldığını yazının devamında bulabilirsiniz.
Faktör analizi çoğu kez araştırmalarda kullanılan çok sayıdaki değişkenin aslında bir kaç temel değişkenle ifade edilebilip edilemeyeceğinin merak edildiği durumlarda kullanılır. Örneğin insanların pek çoğunun günlük olarak aldığı farklı besinler, aslında vücuttaki kullanımları bakımından karbonhidratlar, yağlar ve proteinler olmak üzere üç grupta toplanabilir. Ya da sosyal bilimlerden örnek vermek gerekirse, dil öğrenebilme, bulmaca çözebilme, problem çözebilme, uyaranlara arasındaki küçük farkları ayırdedebilme, ifade yeteneği, olaylar ya da nesneler arasındaki ilişkileri kavrayabilme gibi pek çok zeka göstergesi durum aslında sözel ve sayısal olmak üzere iki zeka grubunda toplanabilir.
Özellikle sosyal bilimlerde yapılan araştırmalarda kullanılan ölçme araçları, bir konunun farklı yönleriyle ilgili sorular barındırmaktadır. Örneğin, psikopatoloji ile ilgili bir araştırma yapan bir araştırmacı, aşağıdaki tablodaki gibi sorular kullanır.
|
Hiç olmaz
|
Nadiren olur
|
Bazen olur
|
Çoğu kez olur
|
Çok sık olur
|
|
|
Titreme
|
|||||
| Kızgınlık | |||||
| Kırıp dökme isteği | |||||
| Baş ağrısı |
burada 4 tane örnek verilmiş olsa da psikopatolojiyi ortaya çıkarmak amacıyla bir ölçme aracında en az 20 madde bulunur (kimi kez bunun 600’e yaklaştığı da olur). Bu örnek maddeler dikkatle incelenecek olursa aslında psikopatolojinin iki boyutu ile ilgili ölçme yaptıkları söylenebilir: Fiziksel belirtiler ve zihinsel belirtiler. Fakat bu oldukça kuramsal ve yoruma dayalı bir yargı olacaktır. Bu maddeler gerçekten uygulandığı kişilerden hangi temel bilgileri getirmektedirler.
Pek çok insanın aklına her bir maddenin tek tek incelenmesi ya da analiz edilmesi gelebilir. Bu ölçeğin bütünün yapmaya çalıştığı şeyden uzaklaşma anlaıma geleceği gibi verilerin bir bütün olarak anlamlandırılmasını da engelleyecektir. Bu durumda, maddeler arası ilişkilerden yola çıkarak o maddelerin birlikte aynı amaca yönelmişliklerini bularak, yani maddeleri aynı işi yapmalarına göre gruplandırarak değerlendirmek daha mantıklı olacaktır. Fakat burada da, “o zaman neden her bir amaç için tek bir madde kullanmıyoruz” sorusu akla gelebilir. Buna verilecek en iyi cevap istatistiksel analizlerin “varyans” a ihtiyaç duymalarıdır. Bir varyans olmadan istatistiksel analizin olması mümkün değildir. Ayrıca tek bir soruyla bir özelliğin (bu örneğin fiziksel psikopatolojik belirtiler gibi bir alt boyut olsa bile) tek bir madde ile örneklenmesi de mümkün değildir.
Bu nedenlerle özellikle sosyal bilimlerde, her bir maddenin hangi diğer maddelerle gruplaşma yaptıklarını (benzer amaca yöneldiklerini), bu maddelerin bu gruplara ne kuvvetle bağlandıklarını görmek amacıyla keşfedici (exploratory) faktör analizi sıklıkla kullanılmaktadır. (çoğunun kullandığı gibi açımlayıcı faktör analizi, exploratory kelimesinin yanlış Türkçeleştirilmesinden başka bir şey değildir).
Faktör analizinin, yapı geçerliliği çalışmaları ile de yakından ilişkisi vardır. Özellikle öçek geliştirme sürecinde geliştirilen ölçeğin ölçülmesk istenen özelliğin hangi boyutlarında ölçme yaptığını ortaya çıkarmak / keşfetmek (explore) ya da halihazırda geliştirilmiş bir ölçeğin gerçekten beklenen şekilde ölçme yaptığını doğrulamak ya da yanlışlamak (confirmatory) amacıyla faktör analizinden yararlanılabilir. Doğrulayıcı (confirmatory) faktör analizi, bir kültürde geliştirilmiş bir ölçeğin başka bir kültüre uyarlamasını yaparken özellikle kullanılabilecek bir geçerlilik kanıtı bulma yöntemidir. Bu yazıda sadece keşfedici (exploratory) faktör analizi uygulamalarından bahsedilecektir.
Keşfedici (Exploratory) Faktör analizi, iki farklı yönteme verilen ortak bir addır. bu yöntemlerden birincisi temel bileşenler analizi diğeri ise faktör analizi olarak adlandırılır. Yani temel bileşenler analizi de faktör analizi adıyla anılmaktadır. Oysa ki temel bileşenler analizi ve faktör analizi, benzer gibi görünen ama farklı amaçlar için hazırlanmış yöntemlerdir.
Peki hangi durumda hangisini kullanmak daha doğru olacaktır?
Eğer amaçlanan, pek çok değişkeni taşıdıkları ortak bilgiye dayanarak bu değişkenlerin bir bileşkesi olarak daha az sayıda değişkenle ifade etmekse (örneğin, 40 soruluk bir içe-dışa dönüklük ölçeğinin maddelerini dışa dönüklüğü ve içe dönüklüğü ölçen maddeler olarak gruplamaksa) temel bileşenler analizini kullanmak daha yararlı olacaktır. Fakat amaç, belirli bir ortak varyansa sahip pek çok değişkenin altında yatan gizil değişkeni tanımlamaksa (örneğin intihar eğilimi, tek boyutlu düşünce, yaşam doyumu, sosyal destek ölçümlerinden hangilerinin depresyon için tanımlayıcı olduğunu bulmaksa) faktör analizinden yararlanılması daha uygun olacaktır.
Temel bileşenler analizi, analize giren değişkenlerin ortak varyansları ve o değişkenlerin özgül varyansları arasında bir ayrıma gitmezken, faktör analizi analize giren değişkenlerin özgül varyanslarını belirleyerek analizden çıkarmaktadır.
Peki faktör analizini uygulayabilmek için neler gereklidir?
Faktör analizi uygulanabilmek için bazı önşartların karşılanmış olmasını gerektirmektedir. Bunlar aşağıda faktör analizinin varsayımları olarak anlatılmışlardır.
Faktör Analizinin Varsayımları:
- Değişkenlerin ölçümleri en az eşit aralıklı ölçek düzeyinde yapılmış olmalıdır (olmadığı durumlar için dummy kodlama ya da çeşitli ölçekleme teknikleri kullanılabilir)
- Değişkenler arasındaki ilişki doğrusal olmalıdır. Değişkenlerin belirli bir düzeyinden sonra diğer herhangi bir değişkenin artışında ya da azalışında, bu düzeyden öncekine ters bir yükselme ya da düşmem bulunmamalıdır. Örneğin kaygı ile başarı örneğinde olduğu gibi çok düşük olduğunda ders başarısının düşük olduğu, kaygının yükseldikçe ders başarısının da yükseldiği fakat belirli bir kaygı düzeyinden sonra ders başarısının yine düşme gösterdiği bir durumda iki değişken arasında eğrisell bir ilişki sözkonudur.
- Çokdeğişkenli normallik (Multivariate normality). İkisi de normal dağılan ik değişkenin oluşturduğu bileşik değişkenin de normal dağılacağına dair bir garanti yoktur. Bu nedenle multivariate normality’nin faktör analizi uygulanmadan önce test edilmesi gerekmektedir
- Sadece Faktör analizi için geçerli olmak üzere faktörlerin birbirleriyle ilişkisiz olması (orthogonality).
- Değişkenlerin altında ortak bir boyutun olması. Birbiriyle hiç bir alakası olmayan konulardan değişkenlerle bir faktör analizi doğru olmayacaktır.
- Değişkenler arasında çok yüksek korelasyonların olması multicollinearity denen birbirinin üstüne binişme durumunu oluşturacağından regresyon analizi içinde yer alan variance inflation factor ile test edilerek multicollinearty sınanabilir.
- Outliers, yan aşaırı uçlardan arındırılmış data. Aşırı uçlar, korelasyon matrisini etkilerek gerçek dışı sonuç elde etme olasılığını artırırlar.
- yeteri kadar örneklem büyüklüğü. Yapılan çalışmalar en azından faktör analizine girecek değişken sayısından daha fazla örneklemden toplanmış verilerle faktör analizi yapılmasını öngörmektedir.
Faktör analizinin SPSS ile uygulamasına geçmeden önce bazı konularda uyarılarda bulunmakta fayda vardır.
- Faktör analizi hem uygulanması hem de yorumlanması açısından uzmanlık gerektiren bir analizdir.
- Bir örnek ile öğretilmesi mümkün değildir. Her bir faktör analizi çalışması başlıbaşına bir süreçtir ve bir süreçte karşılaştığınız durumlar ile diğerinde karşılaştığınız durumlar birbirinden büyük farklılıklar gösterebilmektedir.
- Özellikle maddelerin birden çok faktörde birden ya da negatif yük aldığı koşullarda karar verme süreci daha da büyük önem kazanmaktadır.
Bu nedenle aşağıda verilen örneği faktör analizi sürecinin tamamını öğreten bir örnek olarak görmeyiniz. Yorumlanması ve karşılaşılabilecek özel durumlarla başa çıkılabilmesi için faktör analizi üzerinde uzman bir kişinin gözetiminde bir süre çalışılması gerekmektedir.
Faktör Analizi SPSS programında genel olarak aşağıdaki aşamalardan geçilerek yapılır.
Aşağıda 22 maddelik bir tutum ölçeğinin yapı geçerliliğinin bulunması için yapılan bir faktör analizi örneği verilmiştir.
Veriler aşağıdaki gibi girilmiş olmalıdır. Sadece 22 maddeye verilen cevapların girilmesi yeterlidir. Veriler girildikten sonra genel puanlama yapısının tersine puanlanan madde varsa bu puanların tersine çevrilmesi gerekir. Örneğin bir televizyon dizilerine yönelik tutum ölçeğindeki maddelerin çoğunda anlam hep televizyon dizilerini severim, anlamı içeriyorsa ve 5 puan kesinlikle katılırım anlamına geliyorsa, bu maddeler kendi aralarında puanlama bakımından benzerlik taşıyorlar demektir. Fakat bu maddelerin arasından bir tanesi tutum objesinin karşısında fikir belirtiyorsa, örneğin televizyon dizilerini seyretmeyi aptal işi bulurum maddesinde olduğu gibiyse, ve bir kişi kesinlikle katılıyorum seçeneğini işaretlediyse, daha önceki maddelerde (dizilerin herhangi bir boyutunu olumlu bulma maddelerinde) verdiği kesinlikle katılırım cevabı için alacağı 5 puanların ifade ettiği anlam ile dizileri aptal işi bulma maddesinde verdiği kesinlikle katılırım cevabı için alacağı 5 puan birbirine ters olacaktır.
Şu örneği inceleyin.
|
Kesinikle katılmıyorum |
Katılmıyorum |
Orta derecede katılıyorum |
Katılıyorum |
Kesinlikle katılıyorum |
|
|
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
|
| 1. Dizileri seyretmek için harcanan zamanı boşa gitmiş sayarım |
X
|
||||
| 2. Dizilerdeki karakterlerin davranışlarından olumlu yönde etkilenirim |
X
|
||||
| 3. Diziler olmasaydı yapacak başka bir şey bulamazdım |
X
|
||||
| 4. Dizilerin sayısının arttırılmasının iyi olacağını düşünürüm |
X
|
Yukarıdaki gibi bir cevaplandırmada kişi 1+5+4+5=15 puan alacaktır ama kişinin 1. maddeden alması gereken puan acaba 1 midir? diğer maddelerde dizileri sevdiğini bildiren kişi olumsuz yönde sorulmuş olan 1. maddede de yine dizileri sevme yönünde bir bildirimde bulunmuştur. Yani dizileri seyretmek için harcanan zamanın boşa gitmediğini düşünmektedir. O halde bu madde de diğer maddeler gibi olumlu bir ifade olarak Dizileri seyretmek için harcanan zamanın boşa gitmediğini düşünürüm şeklinde sorulsaydı kişi 5 puan alacaktı. Bu nedenle araştırmaya katılan herkesin 1. maddedeki puanını tersten kodlamak gerekecektir. Bunun için eğer kişi 5 işaretlediyse puanı 1 ile, 4 işaretlediyse puanı 2 ile, 3 işaretlediyse puanı 3 ile, 2 işaretlediyse 4 ile ve 1 işaretlediyse 5 ile değiştirilecektir. Bunun için SPSS’teki recode komutu kullanılabilir. (daha sonra ayrıntılı olarak anlatılacaktır).
Aşağıda anlatılan örnek veri dosyasını http://istatistik.gen.tr/faktor.sav adresinden çekebilirsiniz. Linke sağ tıklayıp farklı kaydet (save as) seçiniz.
Verilerin faktör analizine başlamadan önce spss dosyasında şu şekilde görünmesi sağlanır
Faktör analizi için aşağıdaki spss menüsü açılır
Tıklandığında aşağıdaki diyalog penceresi açılır.
Sağ taraftaki Variables kısmına fatör analizine girecek olan değişkenler ya da maddeler atılmalıdır. Burada 22 maddenin tamamı da faktör analizine sokulacaktır ki aralarındaki ilişkiler bağlamında ölçeğin bütününün faktör yapısı ortaya çıksın. Burası çok önemlidir çünkü Türkiye’de hala Profesör düzeyinden insanlar bu aşamayı kitaplarında yanlış anlatmakta (örneğin maddelerin bir faktör oluşturduğu bilinen bir kısmı girmeliymiş, sonra her bir faktör için bu işlem tek tek yapılmalıymış gibi çeşitli kişisel-efsanevi uydurmalarda bulunmakta ve ve pek çok araştırmacıyı yanlış anaiz yapma ve yanlış bulgu elde etme durumuyla karşı karşıya bırakmaktadırlar. Kaynaklar açıktır. Bu kişilere verilmesi gereken cevap bu yazının en başında giriş bölümünde ayrıntılarıyla verilmiştir.
Faktör yapısı merak edilen ölçeğe dahil olan tüm maddeler sağ taraftaki Varibles bölümüne gönderilir.
Descriptives bölümü tıklanarak maddelere ilişkin betimsel istatistiklerin alınabilmesi için aşağıdaki işasretlemeler yapılır.
Continue tıklanarak önceki pencereye dönülür
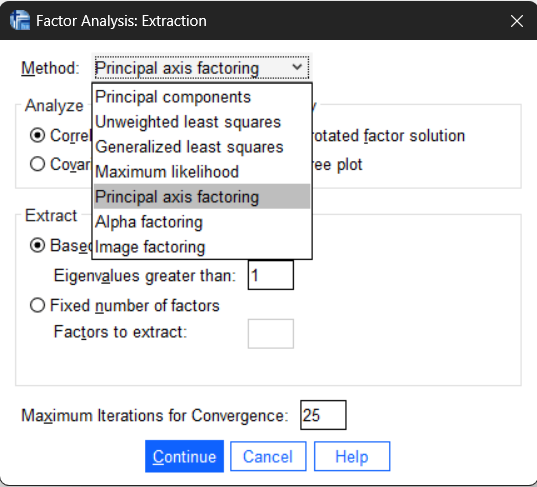
Burada Extraction düğmesine tıklanır. Aşağıdaki gibi bir pencere açılır
Method ile ilgili olarak yazının başında açıklamalar yapılmıştı. Burada araştırmanın amacı maddeleri daha az sayıda faktör ile göstermek olduğundan Principal Axis seçilmiştir. Eigenvalues (özdeğer) over seçeneği 1 olarak öntanımlıdır. Sosyal bilimlerdeki çoğu araştırmada değiştirmeden kalabilir fakat bazı durumlarda number of factors kısmı seçilerek sonuçların kaç faktör ile sınırlandırılacağı belirlenebilir. Bu konu daha sonra ayrıntılarıyla anlatılacaktır. Dikkat edilecek olursa burada hiç bir değişiklik yapılmadı. Buradan Continue tıklanarak devam edilir. Yine biraz önceki ekrana dönülür.
Daha sonra Options düğmesine tıklanır ve aşağıdaki pencere açılır. Değerler faktör analizi çıktısını daha okunabilir, daha derli toplu hale getirebilmek için aşağıdaki gibi değiştirilir.
Yine Continue tıklanarak devam edilir ve faktör analizinin ana ekranına dönülür.
şimdi OK tıklanarak faktör analizinin yapılması sağlanır. Analiz yapıldıktan sonra karşımıza aşağıdaki gibi bir çıktı penceresi gelir.
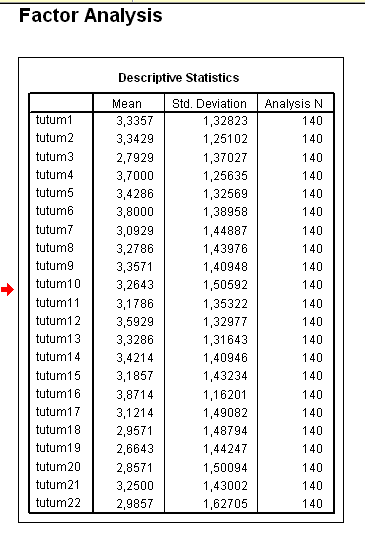
Bu çıktı dosyasının ilk tablosu maddelerin ortalamalarını, standart sapmalarını ve o maddeleri kaç kişinin yanıtadığını gösteren tablodur.
Sayfa biraz aşağıya çekilirse diğer tablolar da görülebilir.
İkinci tablo faktör analizi için önemli olan data-faktör analizi uyumu testlerini göstermektedir.

Kaiser-Meyer-Olkin Measure of Sampling Adequacy değeri, değişkenler tarafından oluşturulan ortak varyans miktarını bildirmektedir. Bu değerin 1,00’a yakın olması datanın faktör analizi için uygun olduğunu gösterirken, 0,50’nin altına düşmesi bu datalar ile faktör analizi yapmanın doğru olmayacağını bildirmektedir. Bu Kaiser-Mayer-Olkin Measure of Sampling Adequacy değerinin örneklem büyüklüğü, kişi sayısı vs gibi, verilerin toplandığı kişi sayısının yeterliliği ile hiç bir alakası yoktur. Bu konuda hiç bir bilgi vermez. Faktör analizi için kişi sayısının yeterli olup olmadığı meselesi ölçülen özelliğin evrendeki heterojenliği, analizin hangi güçte olmasının istendiği, hangi hata düzeyinde yapıldığı, kaç kişiye gidilebilme ihtimalinin bulunduğu gibi çok sayıda faktörün ortak etkisiyle belirlenir. KMO değerinin örneklem büyüklüğü ile hiç bir alakası yoktur.
Bartlett’s Test of Sphericity değeri ve onun anlamlılığı ise değişkenlerin birbirleri ile korelasyon gösterip göstermediklerini sınar. Bu değerin anlamlılığı, yani Sig. (p) değeri 0,10 (sosyal bilimciler 0.05 tercih eder) ve daha üzerindeyse bu datalarla faktör analizi yapmanın uygun olmadığı söylenebilir.
Burada görüleceği gibi iki değer de kullanılan dataların faktör analizi için uygun olduğunu göstermektedir.
Üçüncü tablo ile devam edilebilir.
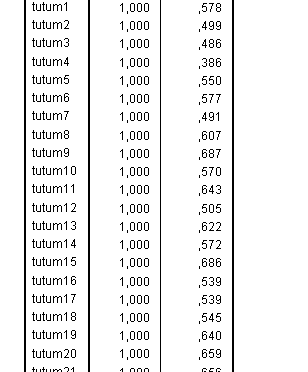
Üçüncü tablo maddelerin içindeki faktöriyel varyansları göstermektedir. Yani her bir maddenin içinde, analiz sonucunda ortaya çıkan faktörlerin varyanslarından ne kadarının bulunduğunu gösterir. Principal components için initial her zaman 1,0’dir. Principal axis metodu seçilirse buradaki 1 değerleri 1’den daha küçük değerler alacaktır. Extraction bölümünde küçük olan değerler o maddenin içinde, maddelerin oluşturduğu ortak varyansın çok küçük bir kısmının bulunduğunu göstermektedir. Büyük olan değerler ise madenin içinde, ölçeğin içindeki maddelerin oluşturduğu ortak varyansının büyük kısmının bulunduğunu gösterir. Küçük değerler analizden çıkarılmalıdır. Ne kadar küçük sorusunun yanıtı daha sonra yanıtlanacaktır.
Biraz daha aşağıya inildiğinde bu maddelerle, ölçülmek istenen değişkenin varyansının % kaçının ortaya çıkarılabildiği görülebilir.
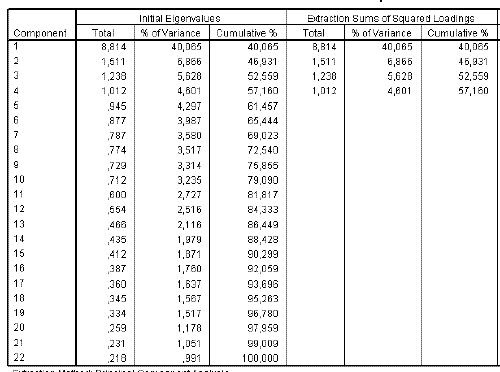
Yukarıdaki resimde görebileceğiniz gibi bu analiz sonucunda özdeğeri (eigenvalue değeri) 1’in üzerinde olan 4 bileşen olduğu saptanmıştır. 1. faktör bu ölçekle ölçülmeye çalışılan özelliğin %40,065’ini açıklarken sırasıyla 2. faktör %6,866’sını, 3. faktör %5,628’ini, 4. faktör ise %4,601’ini açıklamaktadır. Toplamda bu ölçek, ölçülmeye çalışılan özelliğin %57,160’unu açıklayabilmektedir. Bu değerin çok düşük olmaması beklenir. Çünkü açıklanan varyansın düşüklüğü o ölçekle elde edilen bilginin de o denli az olduğu anlamına gelir. Çoğu kaynak bu kümülatif varyansın %50’nin altına düşmemesi gerektiğini söyler. Özellikle doktora tezi çalışması yürütenlerin ölçek geliştirme ya da uyarlama aşamasında buna dikkat etmelerinde oldukça yarar vardır.
Beşinci tablo maddelerin faktör yüklerini, yani hangi maddenin hangi maddelerle aynı değişken altında toplandığını gösteren tablodur.
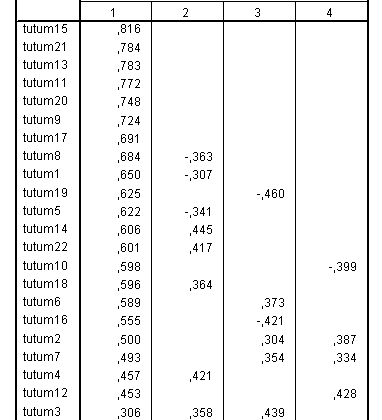
Daha önce dördüncü tablodan da gördüğümüz gibi bu ölçek 4 faktörden oluşmaktaydı. Bunları üstte Components olarak görmekteyiz. Her bir madde, bir ya da daha çok faktör altında toplanabilmektedir. Bu talodaki değerlerin büyüklüğü o maddenin o faktöre o kadar büyük bir güçle ait olduğunu göstermektedir. Örneğin tutum15 maddesi 1. faktöre büyük bir kuvvetle bağlıdır, ya da başka bir deyişle tutum15 maddesi 1. faktörün varyansına büyük katkı sağlamaktadır.
Fakat burada bazı maddelerin tam olarak hangi faktöre ait olduğunu söylemenin zorlaştığı durumlar da vardır. Örneğin tutum7, tutum4, tutum12, tutum3 maddeleri tam olarak hangi faktöre aittir, ya da hangi faktörün varyansına daha çok katkı getirmektedir. Yoksa bunlar altında yük aldıkları tüm faktörlere katkı mı getirmektedirler. Bu duruma bu haliyle karar vermek zor olduğundan faktör analizi sonuçları yukarıdaki gibi (tabii başka koşullar da söz konusu) çıktığında rotasyon adı verilen bir yöntem kullanılır.
Rotasyon, açıklanan varyansı bozmadan daha okunabilir ya da daha uygun bir faktör yapısı bulabilmek için kullanılan bazı yöntemlere verilen genel bir isimdir. Yani birden çok rotasyon yöntemi vardır. Rotasyonda yapılan işleme bir örnek aşağıda gösterilmiştir.
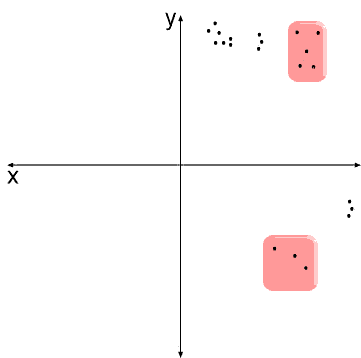
Yukarıda örnek olarak maddelerin x ve y faktörlerinde (bileşenlerine) aldıkları yüklerin kartezyen düzlemdeki durumları verilmiştir. kırmızı ile seçilmiş olan maddelerin durumu yukarıdaki tutum7, tutum4, tutum12, tutum3 maddelerinin durumudur. Bu maddeler x ve y eksenlerine az çok benzer uzaklıktalar. Acaba x bileşenine mi aitler bu maddeler yoksa y bileşenine mi? İşte bu koşulda bu maddelerin okunabilirliklerini arttırmak, uygun bir faktör yapısı yakalamak için rotasyon yöntemlerinden yararlanılır.
Birden çok rotasyon yöntemi bulunmaktadır. Temelde iki grupta toplanabilirler. Doğrusal rotasyon (orthogonal) ve doğrusal olmayan (oblique) Bunlardan sosyal bilimlerde en çok kullanılanları doğrusal rotasyon teknikleridir ve onların içinden de varimax rotasyonu en çok kullanılan yöntemdir. Fakat gerçekte bu yöntemler sosyal bilimlerin doğasına pek uygun değillerdir. Örneğin varimax rotasyonu faktörlerin birbirleriyle korelasyonlarının sıfır olduğunu varsayar ama gerçekte hemen hemen hiç bir zaman faktörler arası korelasyon sıfır değildir. İleride doğrusal olmayan ve varimax dışındaki rotasyon teknikleri de anlatılacaktır. Bu yazıda anlaşılırlığı kolay olduğu için sadece varimax tekniğinden bahsedilecektir.
Yukarıdaki durumda varimax rotasyon tekniği uygulanacak olursa aşağıdaki gibi bir durum gerçekleşir.
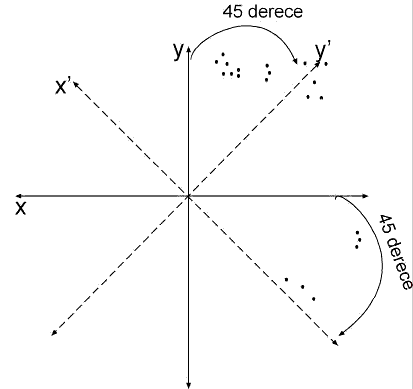
x ve y eksenleri belirli ve birbiriyle olan dik açıları korunarak (burada 45 derece örnek verilmiştir) uygun bir çözüm bulana dek çevrilecek olursa ortaya x’ ve y’ eksenleri çıkar. x’ ve y’ eksenlerine göre maddelerin konumlarına yeniden bakılacak olursa biraz önce kime ait olduğu tam olarak belirli olmayan üstteki kırmızı ile işaretlenmiş maddelerin y’ eksenine yaklaştıkları alttaki kırmızı ile işaretlenmiş maddelerin ise x’ eksenine yaklaştıkları görülür. İşte bu işleme varimax rotasyonu adı verilir. burada verilen örnek sadece iki bileşenli bir örnektir. Bileşen sayısı arttığında işler biraz daha karmaşık hale gelmektedir. İleride bu süreç de anlatılacaktır.
SPSS programı ile faktör analizi uygularken rotasyon işlemi şu şekilde yapılır.
İlk analiz sonunda rotasyona ihtiyaç olduğu ortaya çıkarsa ilk başta kullanılan analiz ekranı Analyse-Data Reduction menüsünden tekrar açılır.
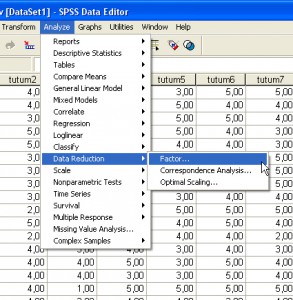
Maddeler sağ tarafa aktarılır ya da önceki analizden sonra spss kapatılıp açılmadıysa tüm maddeler Variables bölümünde bekliyor olur. Burada Rotation düğmesine tıklanarak rotasyon uygulamaları için seçenekler açılır.
Bu pencereden Varimax seçilir ve işaretlemelerin yukarıdaki gibi olduğundan emin olunduktan sonra Continue ile devam edilir ve ana ekrana dönülür.
Burada OK tıklanarak analizin yeniden yapılması sağlanır. Analiz yapıldıktan sonra karşımıza yine aynı analiz çıktısı gelir. Fakat bir farkla. En alttaki component matrix tablosunun altına rotated component matrix tablosu eklenmiş olmalıdır.
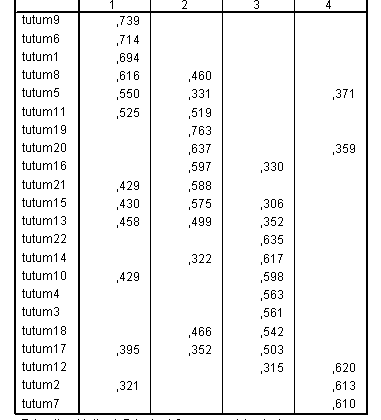
Görülecek olursa yine 4 faktör vardır fakat, maddelerin bu faktörlere dağılımları değişmiştir. Fakat bu noktada tekrar edilmesi gereken bir durum şudur: Rotasyon okunabilirliği arttırmak ya da daha uygun bir yapı bulmak için uygulanan bir yöntemdir. İlk analizde, yani rotasyon olmadan uygun ve sorunsuz bir faktör yapısı bulunduysa analize rotasyonu eklemenin anlamı yoktur.
Şimdi rotasyonlu sonucu inceleyebiliriz.
Tablo incelendiğinde yine bazı maddelerin birden çok faktörde (ya da boyutta) yer aldıkları görülmektedir. Fakat birden çok faktörde yer almalarına rağmen bir faktörde daha çok yer alma eğiliminde oldukları görülmektedir. Örneğin, tutum5 maddesi hem 1. faktörde hem 2. faktörde hem de 4. faktörde yük almıştır. Fakat 1. faktördeki yükü daha fazladır. Peki acaba bir madde aynı anda birden fazla faktörde yük aldıysa o maddeyi, şu faktöre aittir diye sınıflandırabilmek için iki faktördeki yükleri arasında en az ne kadar fark olmalıdır. Bir madde aynı anda birden çok faktörde yük alabilir. Yani bir madde aynı anda hem a konusunu hem de b konusunu ölçebilir. Buna madde düzeyinde çok boyutluluk denir. Bir sorun değildir. Bir maddeden iki işi birden görmesini istemek gibidir. Tıpkı bir matematik sorusunun aynı zamanda okuduğunu anlama becerisini de ölçmesi ile örneklendirilebilir. Fakat burada önemli olan sizin bu matematik sorusundan okuduğunu anlama becerisini ölçmesini isteyip istemediğinizdir. Eğer bunu normal-doğal karşılıyorsanız o madde ölçekte kalmaya devam edebilir. Faktör yükü kadar ölçme yaptığını kabul edip örneğin matematik becerisini 0.616 oranında okuduğunu anlamayı ise 0.460 oranında ölçmektedir, bu nedenle bu maddedeye verilen cevap bu değerlerle ağırlıklandırılacaktır diyerek devam edebilirsiniz. Fakat bu matematik sorusu okuduğunu anlama becerisini ölçmemeliydi, nasıl oldu da ikinci bir faktörde de yük almaya başladı diye endişe ediyorsanız o maddenin ölçekten çıkarılması kararlaştırılabilir. Örneğin tutum8 maddesi hem birinci hem de ikinci faktörde yük almıştır. Buna göre tutum8 maddesi 0.616 değerinde birinci faktöre 0.460 değerinde ikinci faktöre hizmet etmektedir. Bu faktörlerin toplam puanları alınırken tutum8 maddesinin değerleri bu faktör yükleri ile çarpılarak faktör puanlarına döndürülebilir. Ayrıca bu faktör yüklerine dayalı faktör puanları (faktör skorları) bulunarak faktör yükleri ve faktörlerin eigenvektörleriyle ağırlıklandırılmış daha güvenilir puanlar elde edilebilir. Bu konuda ayrıntılı bilgi almak için gizil değişken puanı bulma veya faktör skoru üretme diye arama yapabilirsiniz.
Madde atmaya karar verildiyse atma işlemi faktör analizinde özel bir süreçle yapılmaktadır. Önce maddelerden sadece birisi analize alınmayarak (hatırlayacaksınız ilk ekranda tüm maddeleri analize sokmuştuk, istenmeyen maddeyi sol tarafa geri göndererek madde analize alınmayabilir) faktör analizi tekrar edilmeli, eğer uygun sonuç bulunamazsa atılan madde geri alınmalı, diğer madde analiz dışı bırakılmalıdır. Eğer tek tek madde atmak sorunu çözmezse maddeler ikişerli olarak analiz dışı bırakılmalıdır. Eğer bir maddenin faktör analizi sonucunda atılmasına karar verildiyse o madde artık hiç bir şekilde ölçek içinde bulundurulmamalı ve ölçeğin son halinde yer almamalıdır.
9, 6, 1, 8, 5, 21, 15, 13, 10, 17 ve 2. maddeler ölçeğin birinci faktörünü oluşturmaktadırlar. Bu faktörün adlandırılabilmesi için bu maddelerin yeniden okunması ve hepsinde ortak olan yapı göz önünde bulundurularak bu faktöre bir ad verilmesi gerekmektedir.
8, 5, 11, 13, 14, 18, 19, 20, 16, 21 ve 15. maddeler ölçeğin ikinci faktörüdür.
Diğer faktörlerin belirlenmesi ise size bırakılmıştır.
Sorularınız ve önerileriniz için istatistik@istatistik.gen.tr adresine yazabilir ya da aşağıdaki yorum bölümüne yazabilirsiniz.
Bir yanıt yazın