Açımlayıcı/Kedşfedici faktör analizi ile doğrulayıcı faktör analizi klasik kullanımlarında aynı sonucu vermezler. Açımlayıcı doğrulayıcı analizle aynı sonucu vermeyebilir. Bu yazıda bununla ilgili bir örnek ve ne yapılması gerektiği anlatılmıştır.
Bu konudaki en iyi kaynaklardan birisi Brown’ın Doğrulayıcı faktör analizi kitabıdır. Brown, T. A. (2015). Confirmatory factor analysis for applied research (2nd ed.). The Guilford Press.
Doğrulayıcı faktör analizinden önce açımlayıcı faktör analizi yapmak gerekli mi konusu günümüzün önemli metodolojik problemlerinden birisi oldu. Brown’a göre açımlayıcı sonrası doğrulayıcı faktör analizi genellikle yanlış uygulanıyor. Şöyle ki: Size açımlayıcı analiz yaptığınızda maddeler faktörlere yerleşirken tüm faktörlerde yük alacak şekilde dağılıyor. Oysa doğrulayıcı analizde maddeler sanki sadece bir faktörde yük alıyormuş gibi tanımlıyoruz. Böylece açımlayıcıda elde ettiğimizden çok daha kötü bir modeli doğrulamış oluyoruz. Bu nedenle açımlayıcı yaptıktan sonra doğrulayıcı yapacaksak doğrulayıcı analizde açımlayıcıdan elde edilen faktör yüklerini kullanarak yapmalıyız. Buna e/cfa deniyor. Bu durumda da Brown diyor ki efa ile birebir aynı sonuçları bulacağız. Aynı faktör yükleri, aynı chi-kare değeri aynı rmsea değeri vs. Kitabın 194-202 arası sayfalarında örnekle bunu görebilirsiniz. Peki neden doğrulayıcı yaptık? Zaten birebir aynısı çıkmak zorunda olan bir analizi niçin yaptık? Brown’a göre eğer maddelerin birden çok faktörde aldıkları yüklerin anlamlılıklarını merak etmiyorsanız efa sonrası cfa yapmanın pek bir anlamı yok. Muhtemelen ülkemizde klasikleşmiş “bir madde sadece bir maddede yük almak zorundadır” şeklinde özetlenebilecek olan gereksiz kısıtlamanın yaygınlığı nedeniyle siz de bu efa sonrası cfa’ya ihtiyaç duymayacaksınız. Bu nedenle Brown daha kitabının 1. sayfasında ve 49. sayfasında faktör yapısını önceden biliyorsanız ya da faktör yapınızın ne olduğuna dair güçlü kanıtlarınız varsa “dolaylı olarak” doğrulayıcı yapın diye öneriyor. Siz de bu öneri doğrultusunda hem efa yap hem dfa yap diye ısrar eden hakemlere veya jüri üyelerine dönüş yapabilirsiniz.
Örnek olması açısından buraya tıklayarak örnekteki datayı indirerek hem açımlayıcı/keşfedici hem de doğrulayıcı faktör analizi uygulayabilirsiniz. İki sonucun birbirini tutmadığını göreceksiniz. Keşfedici faktör analizinde 2 faktör elde edeceksiniz. SPSS programında maksimum likelihood yöntemini kullanarak (doğrulayıcı maksimum likelihood kullanıyor o yüzden) faktör analizi uygularsanız şu sonuçları elde edersiniz:
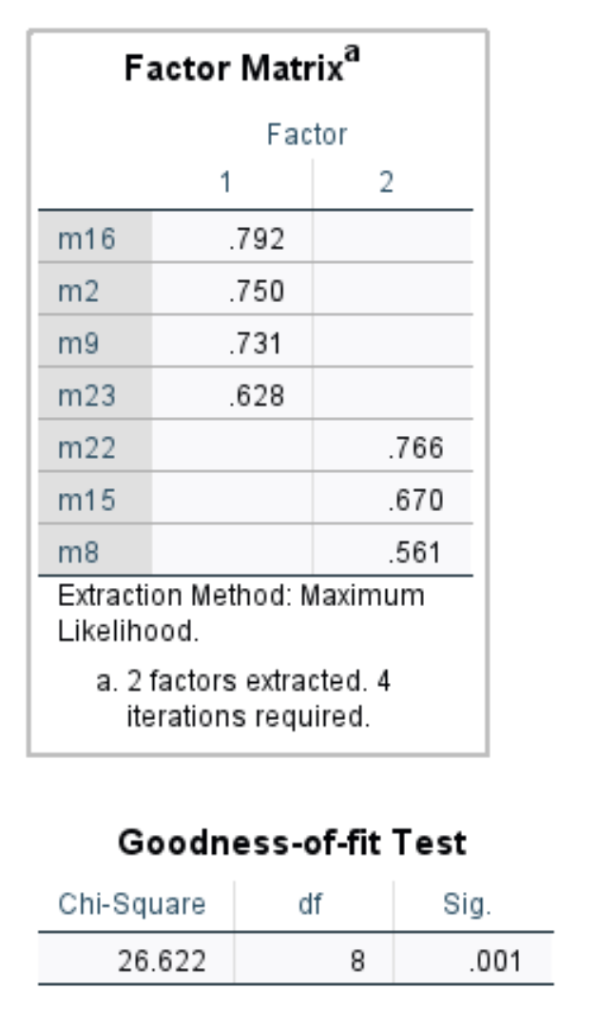
Ardından bu sonuçları yani doğrulatmak için dilediğiniz programı kullanın. AMOS, Mplus, Lisrel, SMART-PLS veya R ile elde edeceğiniz doğrulayıcı faktör analizi sonucunuz ise şöyle olacaktır:
Chi-Square değeri: 65.396, sd = 13, RMSEA = 0.101, CFI = 0.942, TLI = 0.907
Görüleceği gibi özellikle RMSEA değeri modelin doğrulanmasına izin vermemektedir.
Yukarıda yaşanan durum şudur: Keşfedici Açımlayıcı faktör analizinden elde edilen sonuçlar doğrulayıcı faktör analizinde doğrulanmadı.
Fakat bilmelisiniz ki doğrulayıcı faktör analizinde doğrulanmaya çalışılan model açımlayıcıda elde edilen sonuç değildi. Yani yukarıdaki iki analiz aslında birbirini doğrulamıyor. İki analiz birbiriyle aynı modeli kullanmıyor.
Bunun en önemli sebebi, keşfedici faktör analizinde elde edilen faktör yapısının aslında o kadar da saf bir ayrışıklığa sahip olmamasıdır. SPSS gibi programları faktör analizi yaprken madedeleri tüm faktörlere az ya da çok yerleştirir. Yani açımlayıcı keşfedici faktör analzi yaptığınızda her madde az ya da çok bir faktörde yer alır. Yukarıdaki resimde verilen faktör analizi sonucu analiz tekrar edilip de tüm faktör yüklerini göster seçeneği aktive edilerek yapılırsa şöyle görünür:
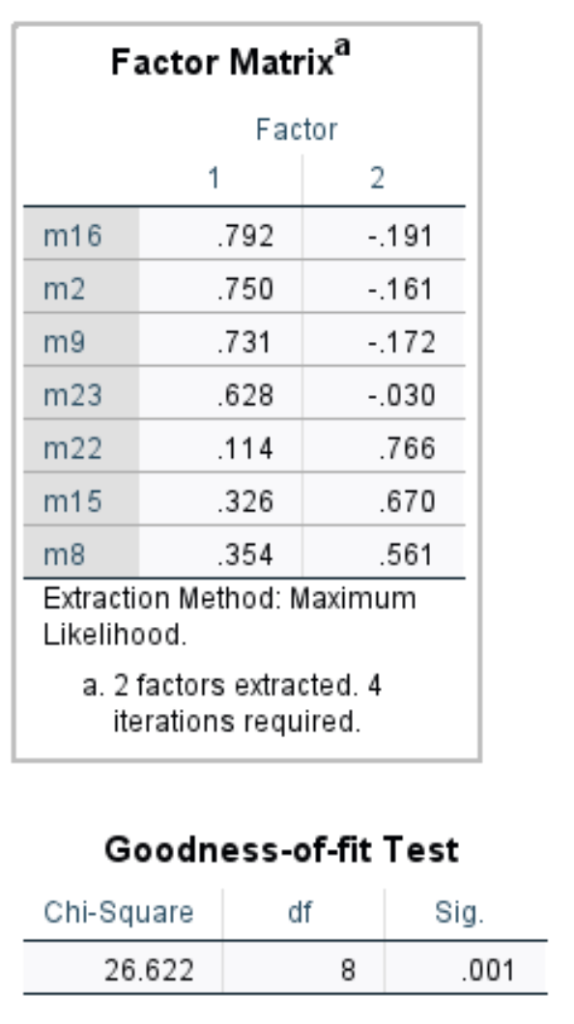
Madde16 aslında iki faktörde de yük almaktadır. İkinci faktörde -0.191 gibi küçük bir yük alıyor ama yine de o faktörde de çalışmaktadır. Siz bunları tamamen gözardı ederek doğrulayıcı faktör analizine geçiyorsunuz ve o madde sanki tek faktörde çalışıyormuş gibi birinci faktörde m2,m9,m16 vardır, ikinci faktörde m8,m15,m22 ve m23 vardır diye düşünerek aşırı berraklaştırma ile doğrulamaya çalışmaktasınız. Dolayısı ile aslında açımlayıcıdan elde ettiğiniz faktör yapısını değil aşırı berraklaştırılmış ve açımlayıcı ile tam olarak uyuşmayan bir modeli doğrulamaya geçiyorsunuz.
Bu aşırı saflaştırma geleneği eski bir gelenektir ve hesaplamaların zor olduğu geçmiş yıllara aittir. Bugün hesaplama kolaylıkları sayesinde bir maddenin birden çok faktörde yük almasına izin verebiliriz. Bir maddenin birden çok faktör alması demek bir maddenin birden çok faktörde ölçme yapabilmesine izin vermek demektir. Tıpkı bir matematik sorusunun hem geometri bilgisini hem de cebir bilgisini aynı soruda ölçmesi gibi düşünebilirsiniz. Gerçek hayatta maddelerimiz her faktörde yük alırken doğrulayıcı analizde sanki böyle bir durum yokmuş gibi davranmak gerçekliğe aykırı olacaktır. Hatta çok daha kötü/alakasız bir modeli doğrulamaya çalışmak olacaktır.
Peki siz açımlayıcıdan elde ettiğiniz şu maddelerin her faktörde az ya da çok yük aldığı “gerçek” modeli doğrulamak istiyorsunuz diyelim. Keşfedici/Açımlayıcı faktör analizinden elde edilen birden çok faktörde yük alma durumlarını da dikkate alan doğrulama işlemi e/cfa olarak da bilinir.
e/cfa bir kaç adımda gerçekleşir:
- (Mümkünse) maximum likelihood kestirim yöntemiyle uygulanmış bir keşfedici faktör analizi sonucunuz olsun.
- Her faktör için çapa madde belirleyin: Çapa madde bir faktörde yüksek yük almışken diğer fakörde sıfıra en yakın yük almış madde demektir. Örneğin yukarıdaki SPSS çıktısı incelenirse birinci faktörde m22, ikinci faktörde m23 maddeleri çapa madde olarak ele alınabilir.
- Bu maddelerin düşük ilgili olduğu faktördeki faktör yüklerini sıfıra sabitleyin
- Maddelerin tümünün tüm faktörlerde yer aldığından emin olun
- faktörlerin faktör varyanslarını 1’e eşitleyin
- Elde edeceğiniz sonucun tüm değişkenler için standardize edilmiş sonuç olmasını sağlayın.
R programında lavaan için kullanabileceğiniz model kodu şöyledir:
model <- 'factor1 =~ m8+m15+m22+m2+m9+m16+0*m23
factor2 =~ m8+m15+0*m22+m2+m9+m16+m23
factor1 ~~ 1*factor1
factor2 ~~ 1*factor2'
ecfa <- cfa(model, data, std.lv=T, std.ov=T)
summary(ecfa, fit.measures=TRUE)
Analizi uyguladığınızda elde edeceğiniz sonuçlar şöyledir:
Chi Square değeri : 26.997, sd = 8, RMSEA= 0.077, CFI = 979, TLI = 0.945
Görüleceği gibi model doğrulandı ve Keşfedici/Açımlayıcı faktör analizi ile elde edilen chi square değeri (çok yakın olacak şekilde) elde edildi.
İşte ancak bu tür bir çalışma/analiz ile keşfedici/açımlayıcı faktör analizinden elde edilen faktör sonucunu doğrulamış olursunuz. Yoksa keşfediciden elde edilenden daha kötü ve gereksiz yere berraklaştırılmış bir modeli doğrulamaya çabalamış olursunuz. Doğrulayabilirsiniz bile, ama doğruladığınız şey keşfediciden elde ettiğiniz bilgi olmayacaktır.
e/cfa yöntemin önemli avantajı size faktör yüklerinizin anlamlılığını da verebiliyor olmasıdır. Normalde SPSS gibi programlar keşfedici/açımlayıcı faktör analizi yaptığınızda sadece faktör yüklerini verirler. Bu faktör yükleri istatistiksel olarak anlamlı olmayabilir. e/cfa sayesinde faktör yüklerinizin anlamlılığını da görebilirsiniz. Aşağıda R programında lavaan çıktısını görebilirsiniz.
Latent Variables:
Estimate Std.Err z-value P(>|z|)
factor1 =~
m8 0.579 0.054 10.767 0.000
m15 0.688 0.054 12.773 0.000
m22 0.774 0.053 14.550 0.000
m2 -0.126 0.066 -1.891 0.059
m9 -0.137 0.066 -2.076 0.038
m16 -0.154 0.068 -2.273 0.023
m23 0.000
factor2 =~
m8 0.269 0.050 5.423 0.000
m15 0.225 0.049 4.630 0.000
m22 0.000
m2 0.769 0.047 16.420 0.000
m9 0.751 0.047 15.936 0.000
m16 0.814 0.046 17.632 0.000
m23 0.628 0.049 12.917 0.000
Keşfedici/Açımlayıcı faktör analizinde elde ettiğiniz faktör yüklerinin birebir aynısını doğrulayıcı faktör analizinde göremeyebilirsiniz fakat iki analiz de aynı kestirim yöntemleriyle elde edilirse faktör yüklerinin birbirine yaklaşması beklenir. Faktör yüklerinin birebir aynı çıkması bekleniyorsa bu durumda lavaan paketi faktör yüklerinin efa’dan elde edilenlerle tanımlanmasına imkan tanımaktadır.
Bir yanıt yazın