Kruskal-Wallis testi ve bir SPSS örneği (Kruskal Wallis Nasıl Yapılır)

K sayıda grup için parametrik olmayan Kruskal-Wallis testi 3 ya da daha fazla grubun/örneklemin aynı evrenden gelip gelmediklerinin belirlenmesi için kullanılır. Bu testin parametrik karşılığı olan tek faktörlü varyans analizi (oneway anova) için gerekli olan varsayımlar (bkz: tek faktörlü varyans analizi) karşılanamadığında, Kruskal-Wallis testi kullanılır

Kruskal-Wallis testinin varsayımları:
a) ıncelenen değişkenin altında sürekli bir dağılım yatmaktadır.
b) ıncelenen değişken, en azından sıralama ölçeği düzeyinde ölçülmüştür.

Eğer sıfır hipotezi doğruysa gruplar arasında sıraların tesadüfi olarak dağılmış olması gerekir

Aşağıdaki şekilde bu durum, A, B ve C gruplarının 1’den 9’a kadar olan sıraları belirli bir kurala göre değil (örneğin A grubundakiler hep düşük sıra numaralarını alması, C grubundakilerin hep büyük sıra numaralarını alması gibi) tamamen rastgele bir şekilde aldığını göstermektedir.

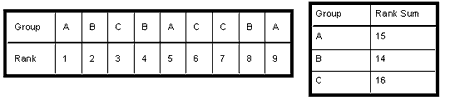
Üç grubun sıra numaraları toplandığında, bu sıra toplamlarının birbirine çok yakın olduğu görülür.

Eğer sıfır hipotezi yanlışsa, gruplar arasında sıralar sistematik bir dağılım gösterir.

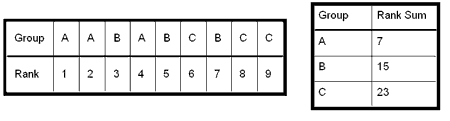
Burada A grubu daha çok düşük sıra numaralarını, C grubu ise büyük sıra numaralarını alıyor görünmektedir. B grubu ise bu ikisinin arasında kalan sıra numaralarını alıyor görünmektedir. Bu grupların sıra numaraları toplandığında, birbirlerinden göreceli olarak daha uzak sıra toplamlarına sahiptirler. Dolayısı ile böyle bir koşulda gruplar arasında fark beklemek daha doğaldır.

Gruplar arasındaki sıra ortalamalarının birbirinden farklı olup olmadığını belirlemek için yapılacak Kruskal-Wallis testinde Kruskal-Wallis değeri aşağıdaki formülle hesaplanır:

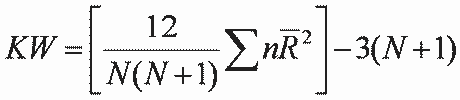
N= Gruplardaki Toplam Kişi/Gözlem Sayısı

= Grup Sıra Ortalaması

n= Her Bir Gruptaki Kişi Sayısı

Aşağıdaki örnekte üç farklı gruptan (akademisyen, politikacı, din adamı) alınmış kontrol odağı puanları bulunmaktadır. Bu üç grubun kontrol odağı puanlarının birbirinden farklı olup olmadığı araştırılmaktadır. Gruplarda çok az sayıda kişi bulunmasından dolayı nonparametrik bir test olan Kruskal-Wallis testi kullanılmıştır.

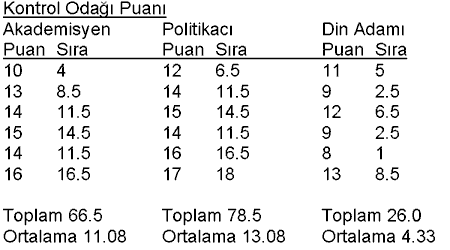
Yukarıdaki Kruskal-Wallis eşitliği bu örneği uygulanacak olursa:

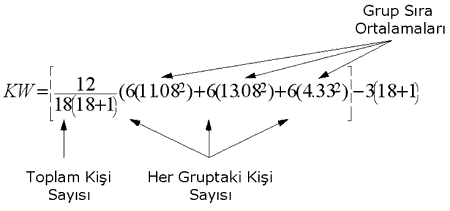
KW= 8,81 olarak hesaplanır. Bu değerin tek başına hiç bir anlamı yoktur. Bu özelliklere sahip (kişi sayısı, grup sayısı) örneklemler için önceden belirlenmiş olan “fark varsa, KW değeri en az şu kadar olmalıdır” bilgisini veren Kruskal-Wallis tablosuna bakmak gerekmektedir. Bu tablodan edineceğimiz kritik değer ile az önce hesapladığımız KW değeri karşılaştırılır. Eğer, “fark vardır” kararı verilmesi için gerekli olan en düşük KW değerini veren tablo değerinden daha büyük bir KW değeri hesaplandıysa bu gruplar arasında, denetim odağı bakımından fark olduğuna karar verilir.

Fakat Kruskal-Wallis testi, karşılaştırılan gruplar içindeki, herhangi iki grup arasındaki farka duyarlıdır. Bir başka deyişle, hesaplanan Kruskal-Wallis değerini, tablo Kruskal-Wallis değerinden daha büyük olması tüm grupların birbirinden farklı olduğu anlamını taşımaz. Kruskal-Wallis grupları topluca değerlendirir, herhangi iki grup arasında (ya da daha fazla grup arasında) fark varsa, anlamlı farklılık bildirir. Fakat hangi gruplar arasında fark olduğunu bildirmez. Bunu bulabilmek için, post-hoc testler denilen karşılaştırmalara ihtiyaç duyulur.

Post hoc test her bir grubu bir diğeriyle karşılaştırır. Bu karşılaştırma için, “iki grup arasında fark vardır kararı verilebilmesi için sıra ortalamaları arasında en az ne kadar fark olmalıdır” sorusuna yanıt aranır. Aşağıdaki formül, Kruskal-Wallis için bu soruyu yanıtlamaktadır.

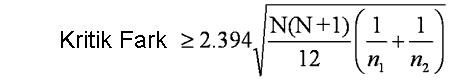
N= Toplam kişi sayısı

n= gruptaki kişi sayısı

Yukarıdaki örnek için hesaplanacak olursa:

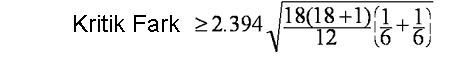
Kritik Fark = 7,38 bulunacaktır.

Demek ki, yukarıda karşılaştırılan grupların sıra ortalamaları arasında 7,38 ya da daha fazla farklılık varsa, bu iki grup arasında “tesadüfen gerçekleşmiş olmayla açıklanamayacak”, anlamlı bir farklılık vardır kararı verilebilecektir. Buna göre:

Din Adamı – Politikacı = 2 < 7,38

Politikacı – Akademisyen = 6,75 < 7,38

Din Adamı – Akademisyen = 8,75 > 7,38

Yukarıda karşılaştırılan üç gruptan sadece Din Adamı ile Akademisyen grupları arasında kontrol odağı bakımından anlamlı bir farklılık bulunmaktadır. Din Adamı ve Politikacı ile Politikacı ve Akademisyen grupları denetim odağı bakımından birbirine denktir.

şimdi de SPSS kullanarak Kruskal-Wallis testinin nasıl uygulanacağını görelim.

Verilerimiz, en basit haliyle spss dosyamızda şu şekilde görünmelidir.

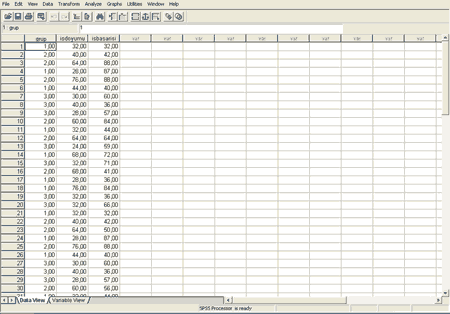
Analiz için Üstteki Analyse menüsüne girerek Non-parametric tests bölümü açılmalıdır. Açılan menüden ise k independent samples (k sayıda bağımsız örneklem) menüsüne girilmelidir. Aşağıdaki resimde bu yol gösterilmiştir.

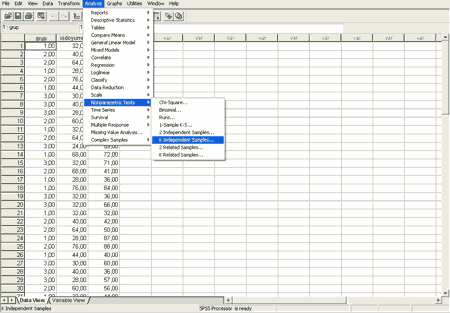
Buraya tıklandığında aşağıdaki pencere açılır:

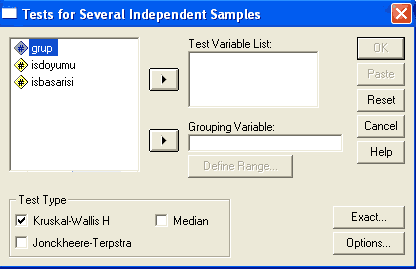
Bu pencerede Grouping Variable yazan kısma grupları gösteren değişken Test Variable List kısmına ise gruplar arasında hangi değişken bakımından fark aranıyorsa o değişken atılır. Aşağıdaki resim bu süreci göstermektedir.

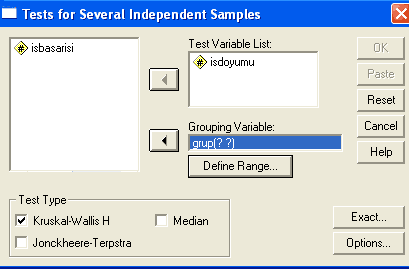
Gruplama değişkeni atıldıktan sonra hemen altındaki Define Range seçeneği aktif olarak, grup(? ?) şeklinde bir durum ortaya çıkmıştır. Burada Define Range düğmesine tıklayarak, kaç grup olduğunun SPSS’e bildirilmesi gerekmektedir. Aşağıdaki resim bunu göstermektedir:

Burada Minumum kısmına 1, Maximum kısmına ise 3 yazarak 1 ile 3 kodu arasında kalan gruplar da dahil olacak şekilde analiz yapmak istediğimizi SPSS’e bildirmiş olduk.

Böylece bu örnekte, 1, 2 ve 3 kodu verilmiş olan deney (1), kontrol (2) ve izleme (3) grupları arasındaki farkın incelenmesi sağlanmış olacaktır. Continue tıklanarak devam edilir. Karşımıza şu pencere çıkar:

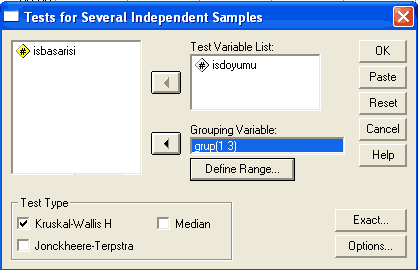
Burada Options düğmesine tıklanarak açılan pencereden Descriptives seçeneği işaretlenir

Yine Continue tıklanarak devam edilir. Son olarak karşımızda şu ekran kamıştır. Artık OK tuşu tıklanarak analiz yapılabilecek duruma gelinmiştir.

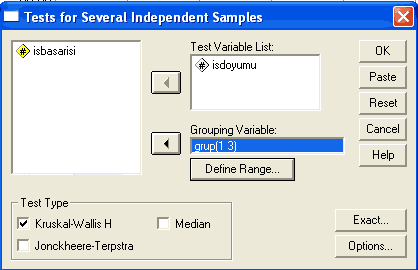
OK tıklandığında analiz yapılır ve SPSS bize şu çıktıyı verir:

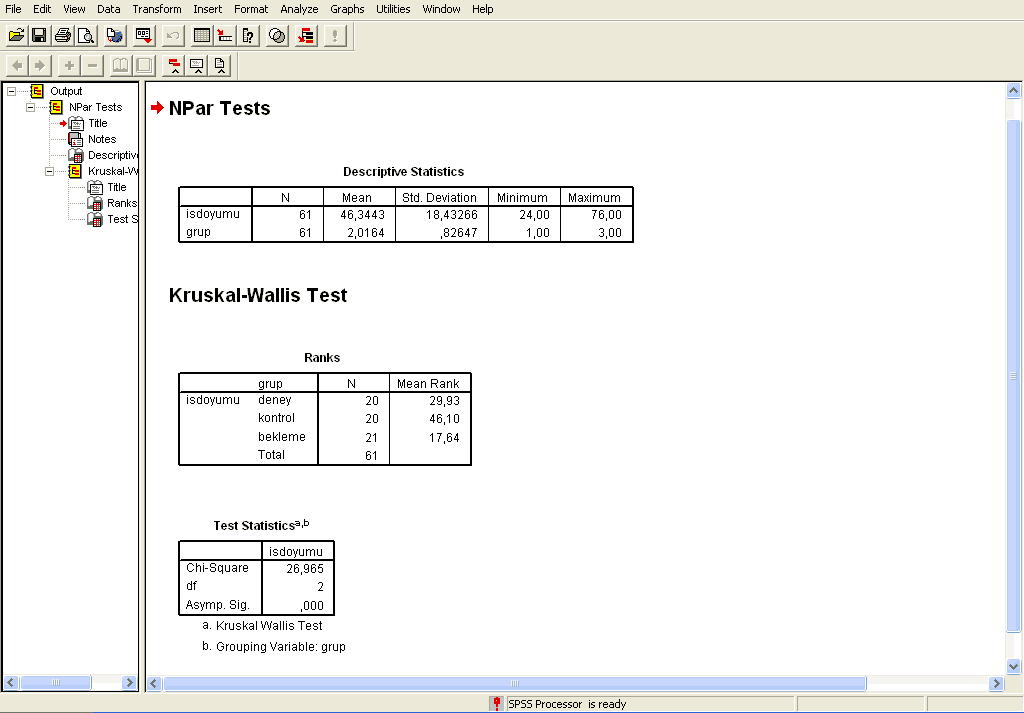
Burada ilk iki tablo betimsel istatistikleri bildirmektedir. Gruplarda kaçar kişi bulunduğu, bu grupların sıra ortalamaları gibi. Karar vermemizi sağlayacak olan tablo Test Statistics tablosudur. Chi-Square olarak görünen değer, daha önce yukarıda formülle hesaplamış olduğumuz Kruskal-Wallis (KW) değerine denk gelmektedir (ıki örnekte değerlerin farklı olması, bu örneklerin farklı araştırmalar olmasındandır). SPSS, bizim için gerekli olan tablo karşılaştırmasını kendisi yapmakta ve bu karşılaştırma sonucunda, “sıra ortalamaları arasında anlamlı fark yoktur” deme olasılığını Asym. Sig (Asymptotic Significance) ile bildirmektedir. Eğer bu değer, 0,05’e eşit ya da daha küçükse, karşılaştırılan sıra ortalamalarından en az ikisi arasında, istatistiksel açıdan önemli (manidar) yani anlamlı bir farklılık vardır kararı verilebilir. Eğer bu değer 0,05’ten daha büyükse, bu grupların sıra ortalamalarının hiç birisi arasında anlamlı farklılık yoktur, bu gruplar birbirine denktir kararı verilebilir. Fakat unutulmamalıdır ki bu karar %5 yani 0,05 düzeyinde alınmış bir karardır. Yani, bu kararın %5 olasılıkla yanlış olması ihtimali bulunmaktadır.

Soru ve önerilerinizi aşağıdaki yorum bölümüne yazabilirsiniz